Exploring Quantum Annealing: A Specialized Approach
Understanding the Fundamentals of Quantum Annealing
Quantum annealing provides a distinctive quantum computing pathway for optimization challenges. Rather than systematic searches characteristic of classical methods, it employs quantum principles to simultaneously explore extensive solution spaces. This probabilistic examination might reveal solutions beyond classical computational reach.
The process essentially manipulates a quantum system's energy landscape, guiding it toward the lowest energy configuration. Similar to physical cooling processes, controlled annealing schedules enable effective solution space navigation, facilitating optimal or near-optimal solution identification.
Quantum Annealing vs. Classical Optimization
Where classical methods like gradient descent follow linear paths often trapped in local minima, quantum annealing explores multiple possibilities concurrently. This inherent parallelism offers potential advantages for complex optimization landscapes where classical approaches falter.
The fundamental distinction lies in methodology: classical techniques rely on sequential calculations while quantum annealing utilizes superposition and entanglement for probabilistic space exploration. This parallelism could prove significantly faster for large-scale optimization challenges.
Applications of Quantum Annealing in Optimization Problems
Quantum annealing's broad solution space exploration makes it promising for logistics, materials science, financial analysis, and drug development applications. Its capacity for handling multi-variable problems represents a major strength, from supply chain optimization to material property design and investment portfolio management.
Machine learning also benefits, where annealing can optimize parameters and enhance model performance, demonstrating remarkable versatility as an optimization tool.
The Quantum Hardware Required for Quantum Annealing
Specialized quantum annealers, distinct from general-purpose quantum computers, are essential for quantum annealing implementation. These devices feature architectures specifically designed for efficient energy landscape manipulation during annealing processes.
Superconducting circuits commonly form the physical basis for these annealers. Hardware design refinement remains critical for addressing increasingly complex optimization challenges.
Challenges and Limitations of Quantum Annealing
Despite its potential, quantum annealing faces notable constraints. Its applicability remains problem-specific, necessitating careful suitability assessment. Current annealer generations have limitations regarding problem scale and complexity, while the algorithm's probabilistic nature introduces solution quality uncertainties.
The Future of Quantum Annealing in Optimization
As quantum hardware progresses, quantum annealing's optimization potential expands. Continued hardware improvements and algorithmic innovations may enable solutions to currently intractable problems across materials science, finance, and logistics, establishing annealing as a valuable optimization resource.
Quantum Algorithms Beyond Annealing: Variational Quantum Algorithms (VQAs)
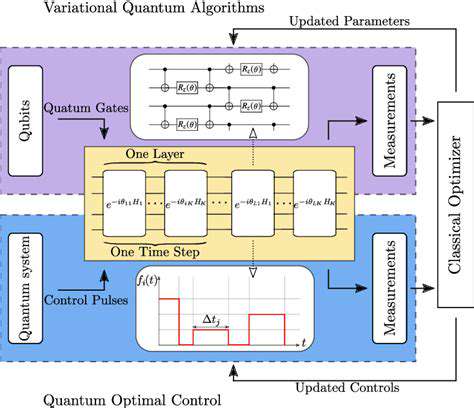
Quantum Algorithms for Optimization
While quantum annealing serves specific optimization needs, Variational Quantum Algorithms (VQAs) provide more flexible frameworks. These algorithms adapt to diverse optimization landscapes through iterative quantum circuit parameter adjustments, potentially outperforming annealing approaches. This adaptability proves particularly valuable for problems not conforming to the Ising model framework common in annealing algorithms.
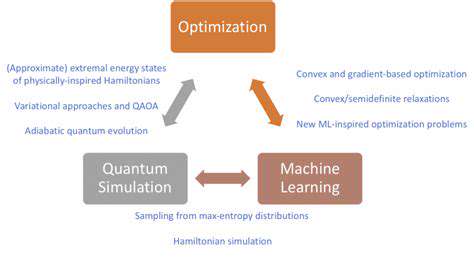
Quantum Simulation and Materials Science
Quantum computers excel at quantum system simulation, offering materials science capabilities beyond classical methods. This enables discovery of novel materials with tailored properties for applications ranging from catalysis to solar energy and advanced electronics.
Quantum Machine Learning
Emerging quantum algorithms show promise for accelerating certain machine learning tasks, particularly those involving complex data structures. Early results in classification and feature extraction suggest potential advantages over classical methods in specific applications.
Quantum Cryptography and Security
Quantum principles enable fundamentally secure cryptographic methods resistant to quantum computing attacks. Quantum key distribution represents a major advancement for secure digital communications in our increasingly interconnected world.
Quantum Algorithms for Drug Discovery
Molecular simulation capabilities could transform pharmaceutical research. Accurate quantum modeling of molecular interactions might accelerate drug candidate identification, potentially revolutionizing treatments for complex diseases.
Applications and Case Studies: Quantum Optimization in Action
Applications in Financial Modeling
Quantum methods enable sophisticated financial analyses through large dataset handling. This facilitates detailed simulations crucial for investment strategy development and risk evaluation across various financial instruments.
Case Studies in Healthcare
Healthcare applications range from resource optimization to treatment improvement. Predictive modeling of patient admissions has demonstrated significant operational efficiencies, while molecular analysis accelerates therapeutic development.
Implementation in Supply Chain Management
Quantum optimization enhances supply network analysis, identifying efficiency improvements. Demand forecasting capabilities enable proactive inventory management, reducing operational costs.
Applications in Environmental Science
Environmental data analysis benefits from quantum approaches, identifying climate patterns and pollution trends. This supports evidence-based policy development and environmental protection strategies.
Quantum in Retail and E-commerce
Customer data analysis enables personalized marketing and inventory optimization. These applications enhance engagement while reducing excess inventory costs.
Beyond the Basics: Advanced Applications
Quantum methods extend to risk management, fraud detection, and customer relationship applications. Advanced modeling capabilities and unstructured data handling expand potential use cases across industries.
Current Challenges and Future Directions
Economic Volatility and Uncertainty
Global economic fluctuations necessitate adaptable business strategies. Market unpredictability requires careful resource allocation and flexible operational models to navigate changing conditions.
Technological Disruption and Innovation
Rapid technological advancement demands continuous adaptation. Investment in emerging technologies and workforce development ensures sustained competitiveness.
Environmental Sustainability and Climate Change
Sustainable practices are increasingly critical for business operations. Resource efficiency and renewable energy adoption align with regulatory requirements and consumer expectations.
Social and Political Instability
Global operations require nuanced understanding of local contexts. Effective risk management strategies account for geopolitical and social dynamics.
Skills Gap and Workforce Development
Addressing workforce skill shortages is essential for business continuity. Comprehensive training initiatives and competitive compensation attract necessary talent.
Resource Scarcity and Access to Capital
Resource competition impacts operational costs. Supply chain resilience and alternative resource exploration mitigate these challenges, while capital access remains crucial for growth.
Global Interconnectedness and Collaboration
International cooperation addresses shared challenges. Cross-cultural understanding facilitates effective global operations and joint problem-solving initiatives.